数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
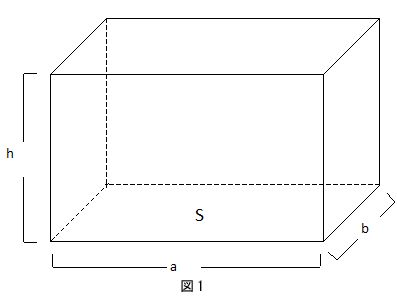
正四角錐の体積の求め方には公式があるんだ。 正四角錐って底面が正方形で、先がとんがっている立体のことだったよね。 底面の1辺の長さをa、高さをhとすると、体積はつぎのようにあらわせるよ。 1/3 a²h つまり、 (底辺の1辺)×(底辺の1辺)×(正四角錐の高さ)÷3 ってことだね。 今日は、この計算公式をどうやって使うのか? ? ということをわかりやすく解説していくよ。 正四 四角柱の側面積 底辺×高さ×4 四角柱の側面積 底面積×2+底辺の長さの合計×高さ 頑張って下さいf (^^;
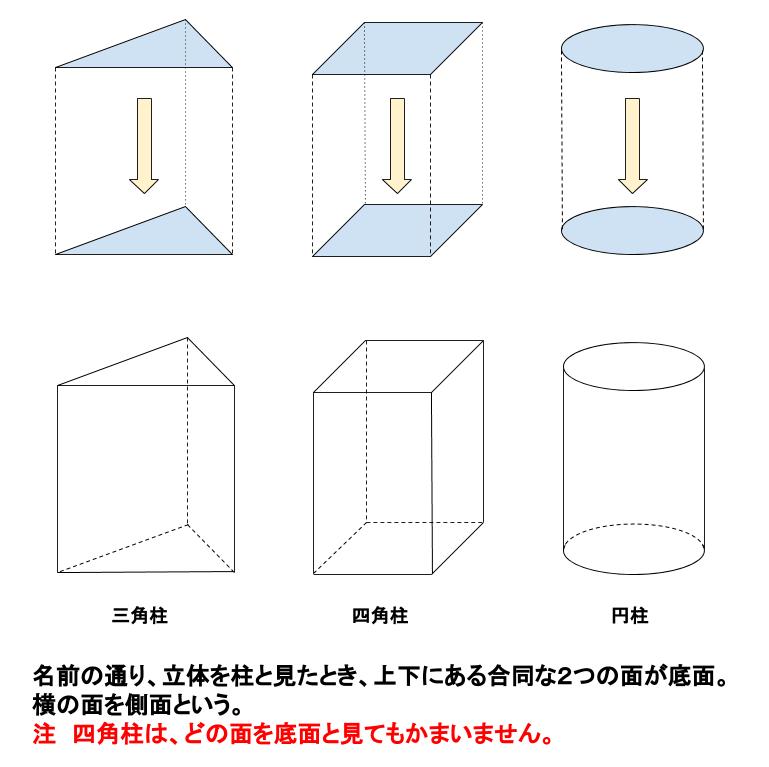
四角柱 体積の求め方
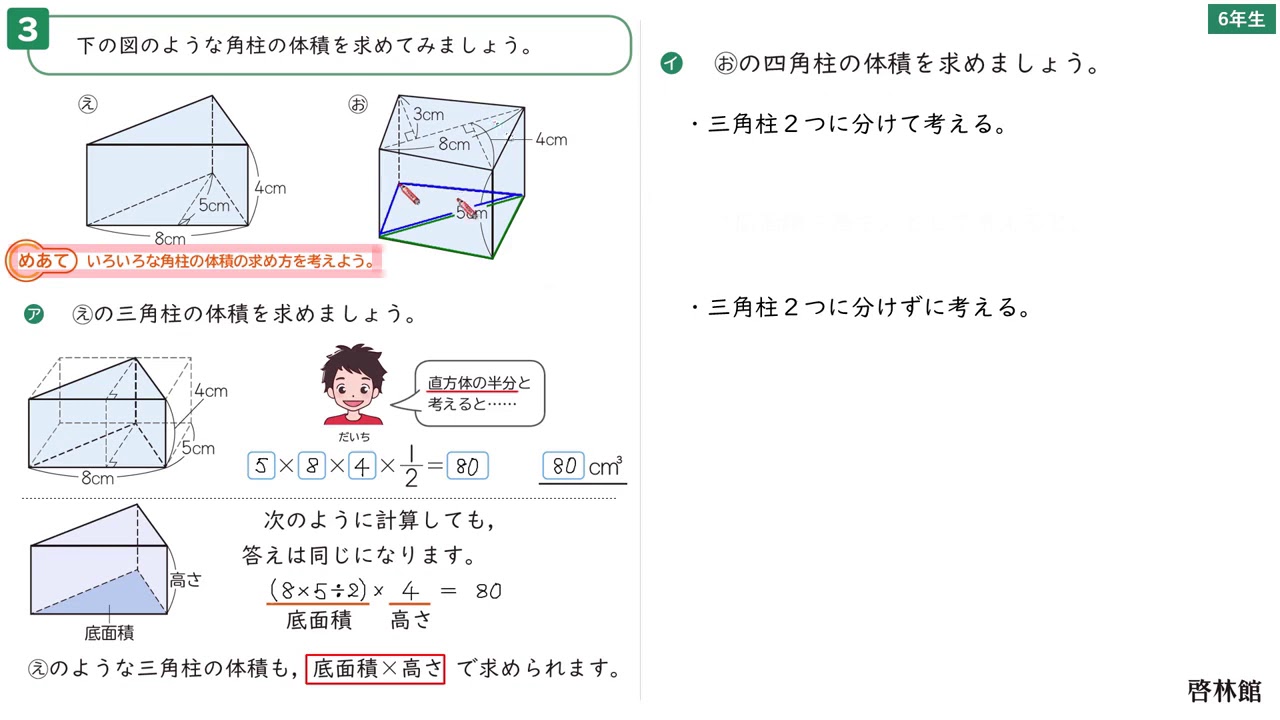
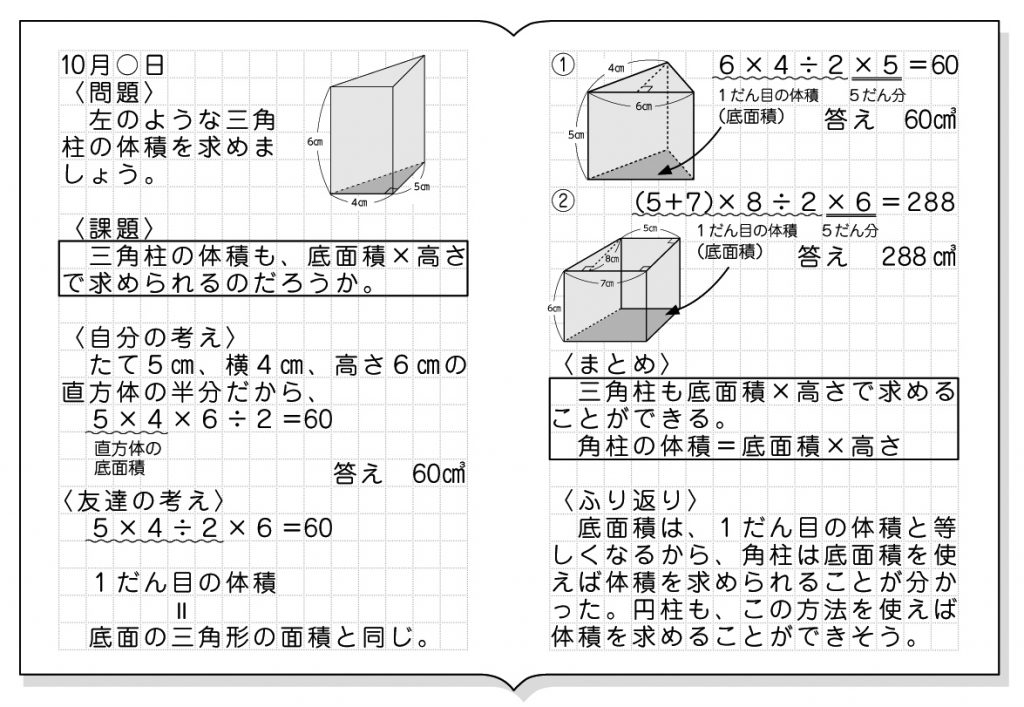
四角柱 体積の求め方-体積を求めるには、これに高さをかければよいので、 5 × 4 = c m 3 が答えとなります。 四角柱の体積 四角柱の場合も考え方は同じです。 底面積を計算するのが三角柱の場合よりも少しだけ大変です。 例題2:図のような四角柱の体積を求めよ。 (底面は台形、上底が 2 c m 、下底が 6 c m 、台形の高さは 3 c m 、四角柱の高さは 4 c m ) この場合、底面は台形なので、その面積は、 ( 2 6) × 3四角柱の体積の求め 方を,直方体の体積 の求め方を基に類推 し,図や式を用いて 考え,説明すること ができる。 24だけを見ると、別の意味もある。 縦×横は、底面積を求めることにもなる。 = 1(㎤) 上のように考えると,四角柱の体積は底面積×高さ
算数流体積の求め方 Sciencelab 冨田塾
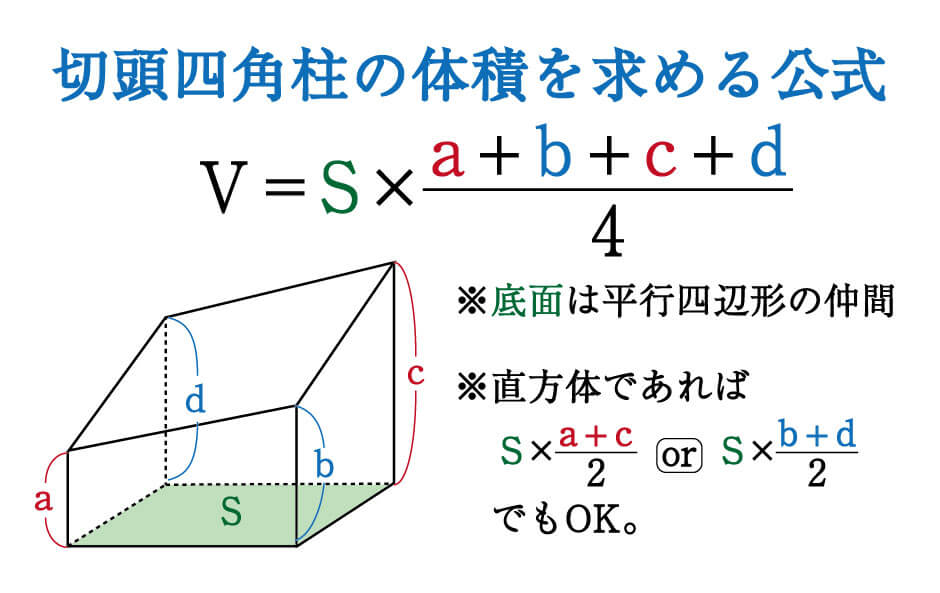
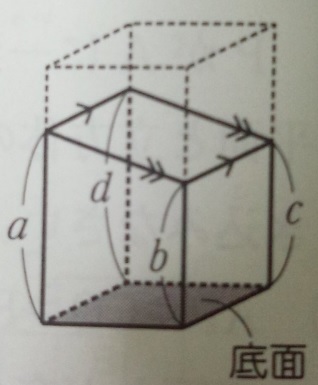
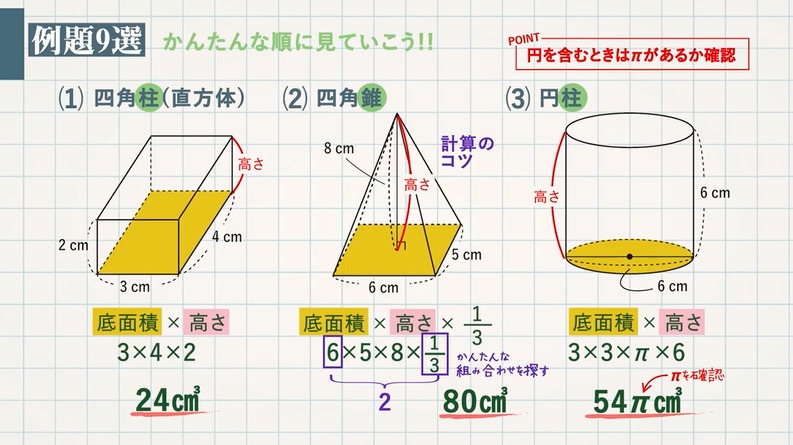
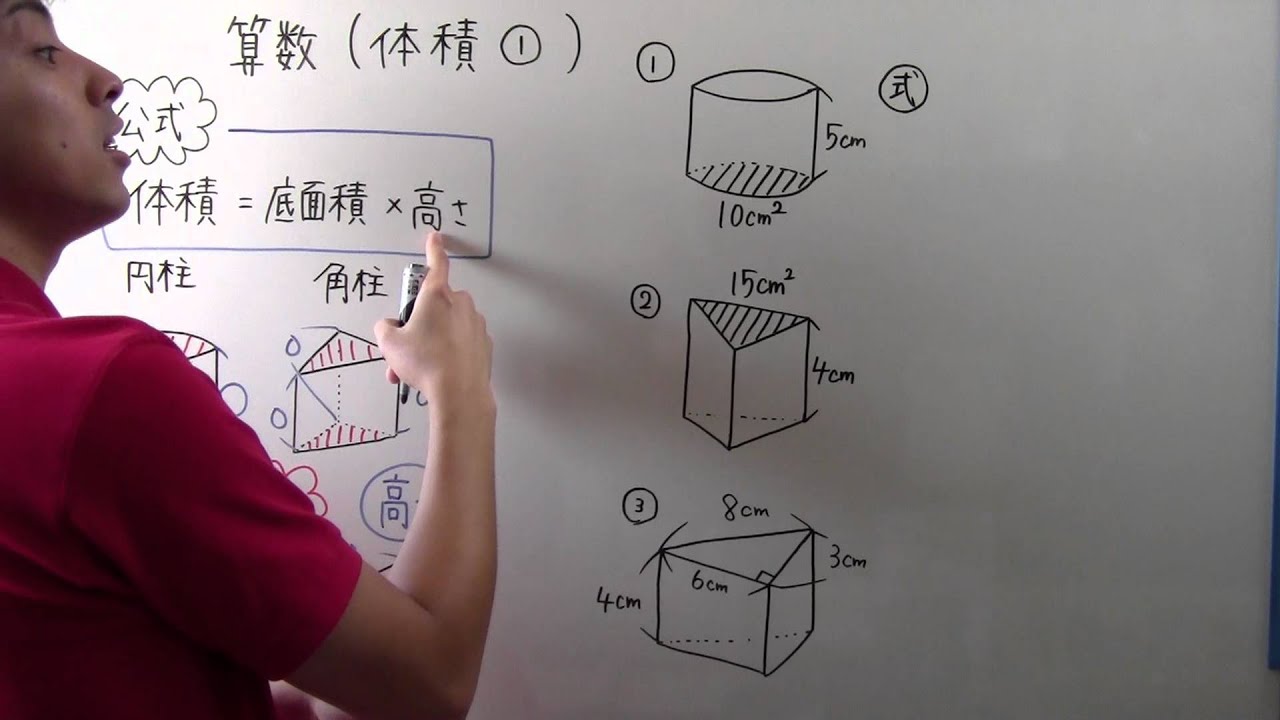
柱体に関して、その体積を求めるには、以下の公式によって求めることができます。 公式 四角柱の体積=底面積(底面の四角形の面積)×高さ したがって、底面の四角形の面積さえ求めることができれば、簡単に四角柱の体積を求めることができるでしょう。 体積を求める上でのポイント 注意が必要なのは、この底面積たる四角形の面積を求める際に、しっかりとそれを導くこと 1:高校受験数学の問題で、四角柱の頭部を切断した残り部分の体積を求める公式として 底面積x (abcd)/4(abcdはそれぞれ底面に垂直な辺の長さ) つまり、体積=底面積☓底面に垂直な辺の長さの平均 があるそうですが、なぜそうなるのですか? 同じ立体柱や円柱の体積の求め方を考 える。 ・第5学年で学習した直方体や立方体の求め方を基にして,四角 柱や三角柱の体積を求めるために,第5学年の教科書を振り返 る。 2 3 四角柱(直方体)の体積の 求め方を「底面積×高さ」と 見直し,底面が直角三角形の
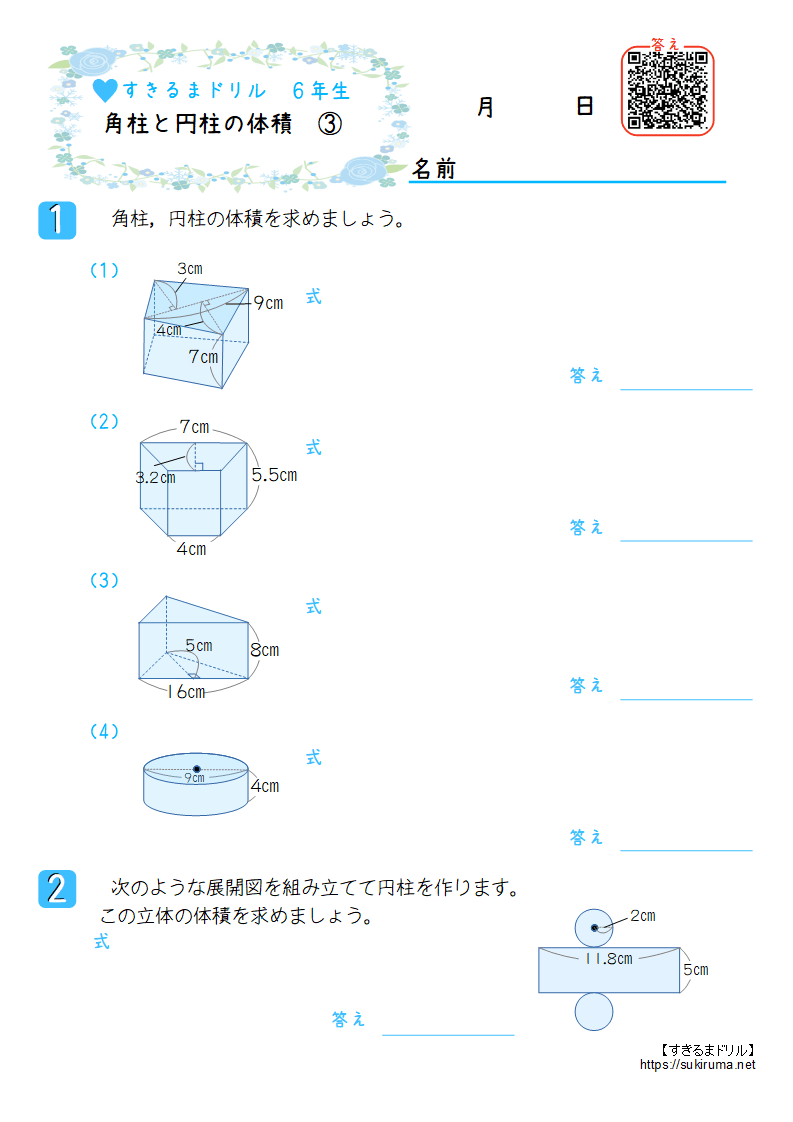
(ひし形ABCDの面積 )=(長方形EFCA) = (長方形EFGH)÷2 = (対角線)×(対角線)÷2 になるんだ。 底辺と高さをつかった菱形の面積の公式 つぎは、「底辺」と「高さ」をつかった公式だよ。 菱形の面積は、 (底辺)×(高さ) で計算できちゃうんだ。 公式をつかってみよう! たとえば、つぎのような菱形ABCDだね。 底辺:10cm 高さ:12cm のひし形だとすると、こいつの四角柱(直方体)の求め方を基に,角柱や円柱の体積の求め方を理解し,解くことができる。 5 単元の評価規準 関心・意欲・態度 数学的な考え方 技能 知識・理解 角柱や円柱の体積の 公式を導き出そうとし ている。 角柱や円柱の体積の2 次の展開図を組み立てて、できあがる立体の体積を求めましょう。 ① 式 長方形の横の長さは、円周と同じ長さなの
四角柱 体積の求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | ||
 | ||
「四角柱 体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「四角柱 体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「四角柱 体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「四角柱 体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「四角柱 体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「四角柱 体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「四角柱 体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「四角柱 体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
「四角柱 体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「四角柱 体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「四角柱 体積の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
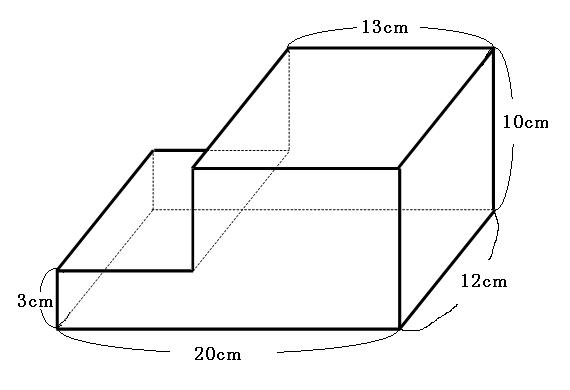
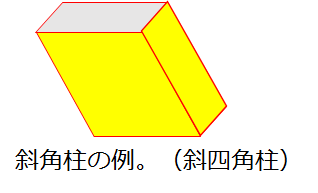
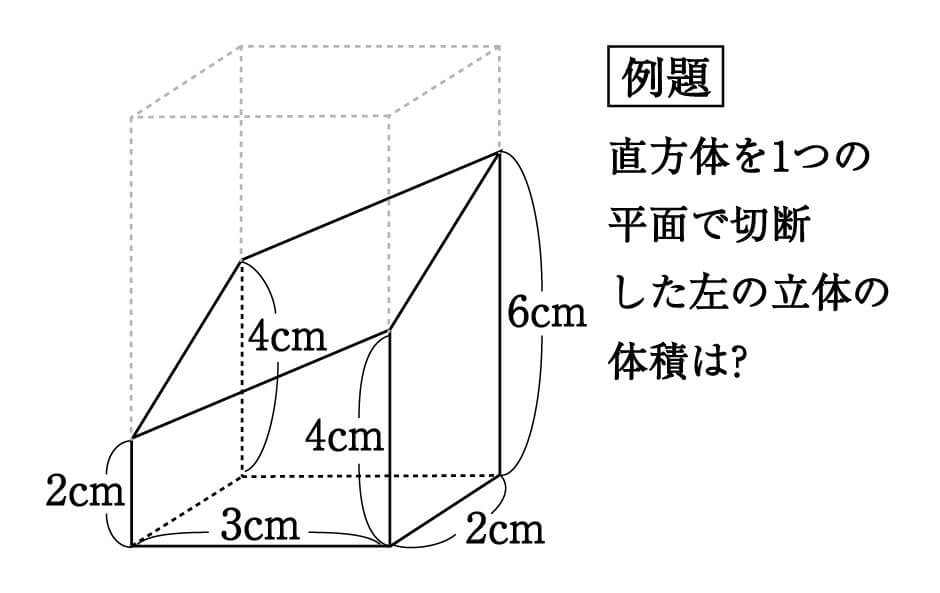
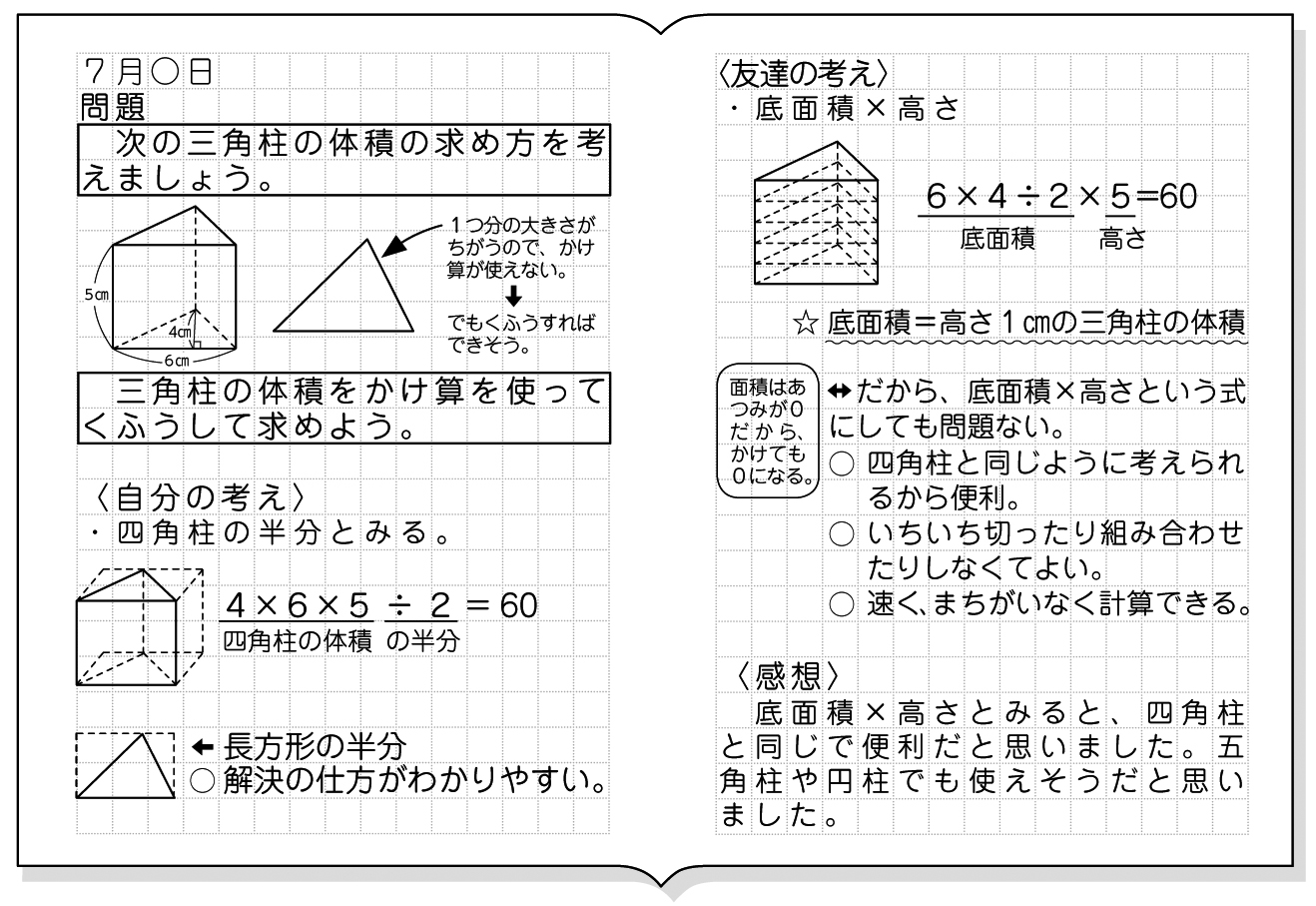
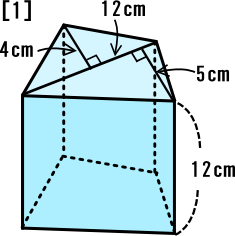
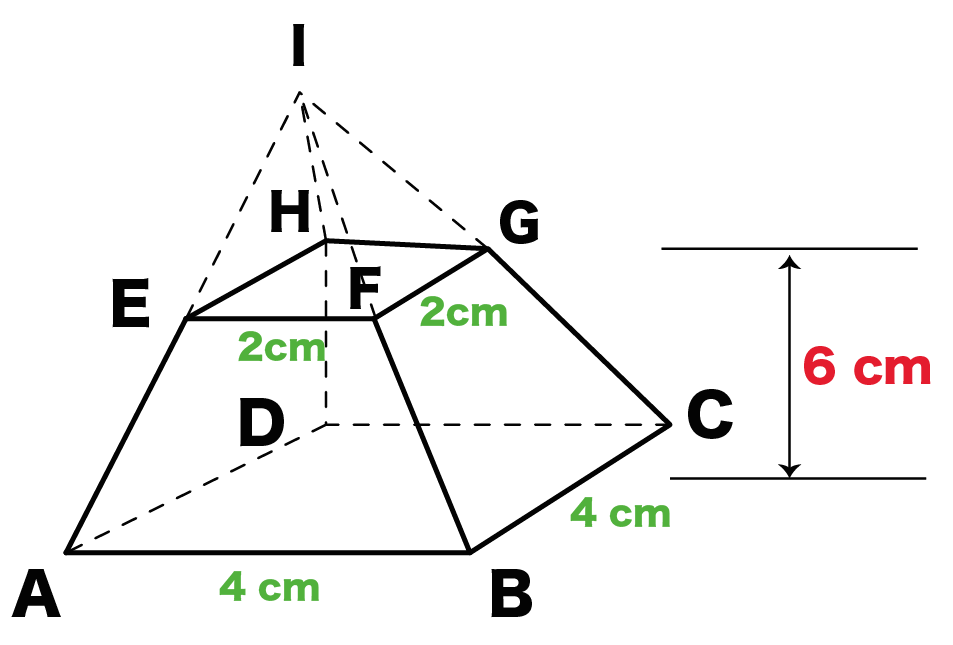
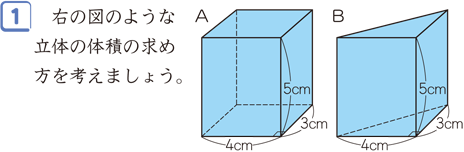
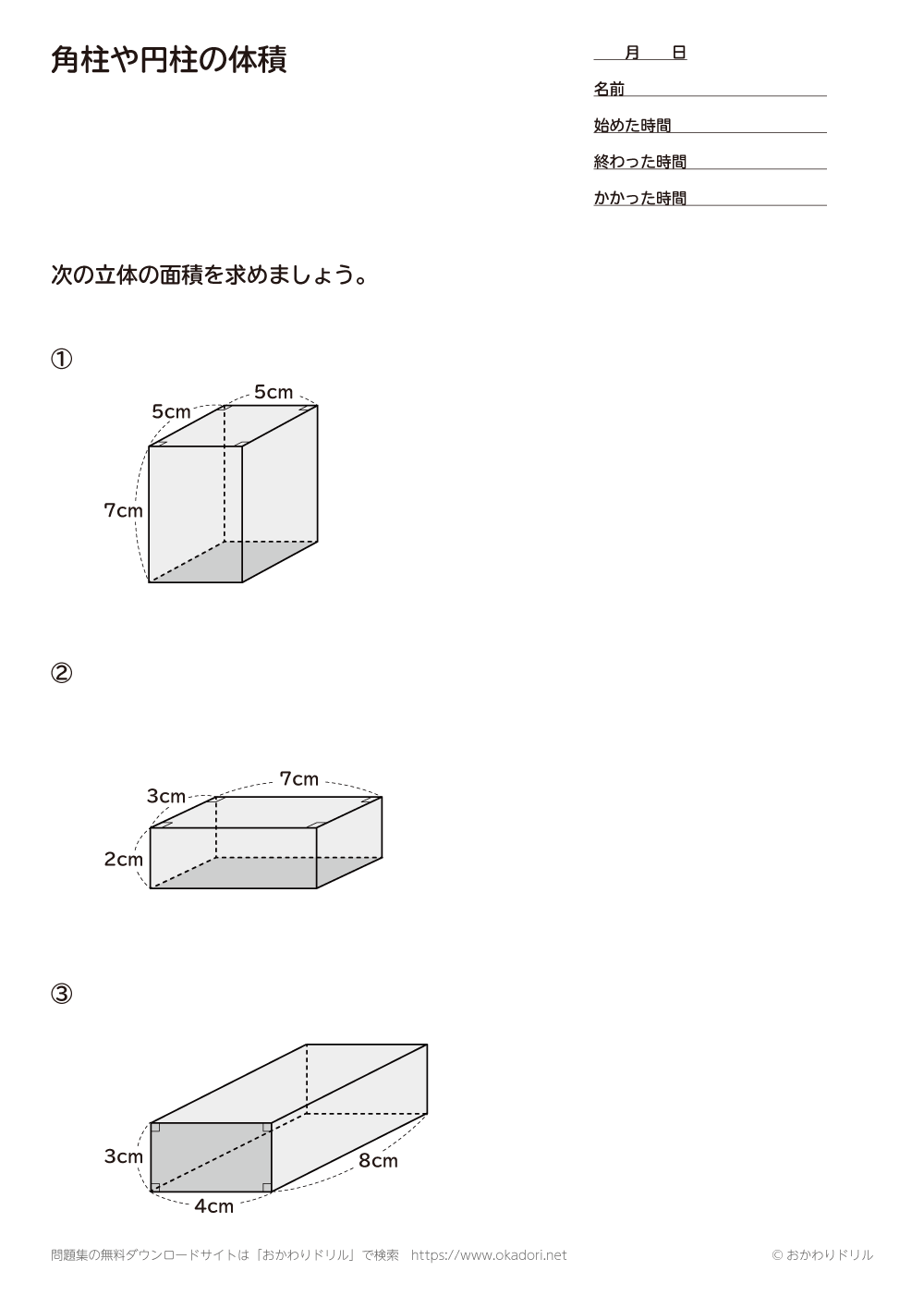
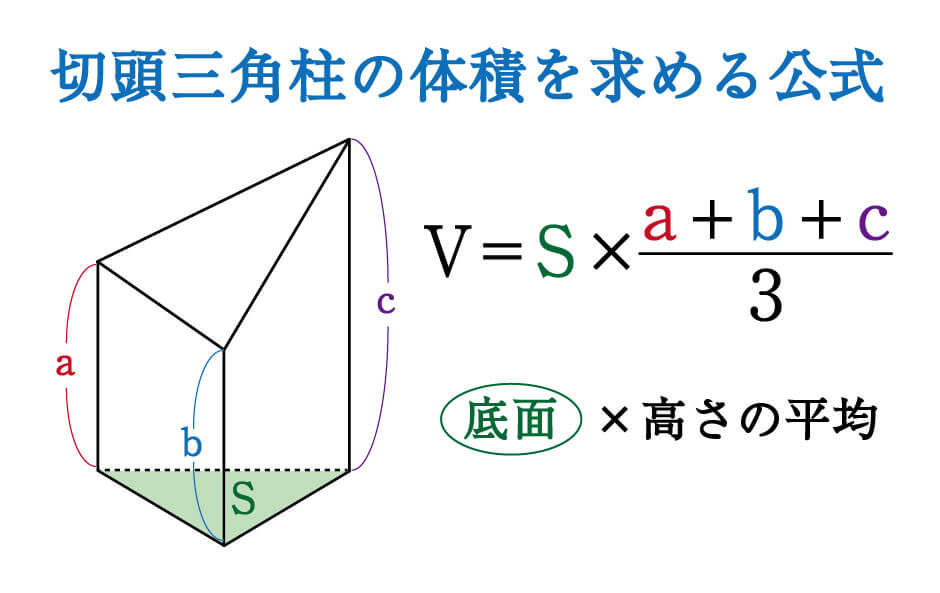
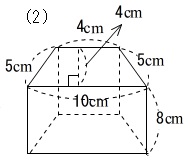
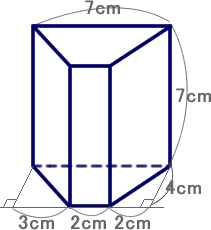
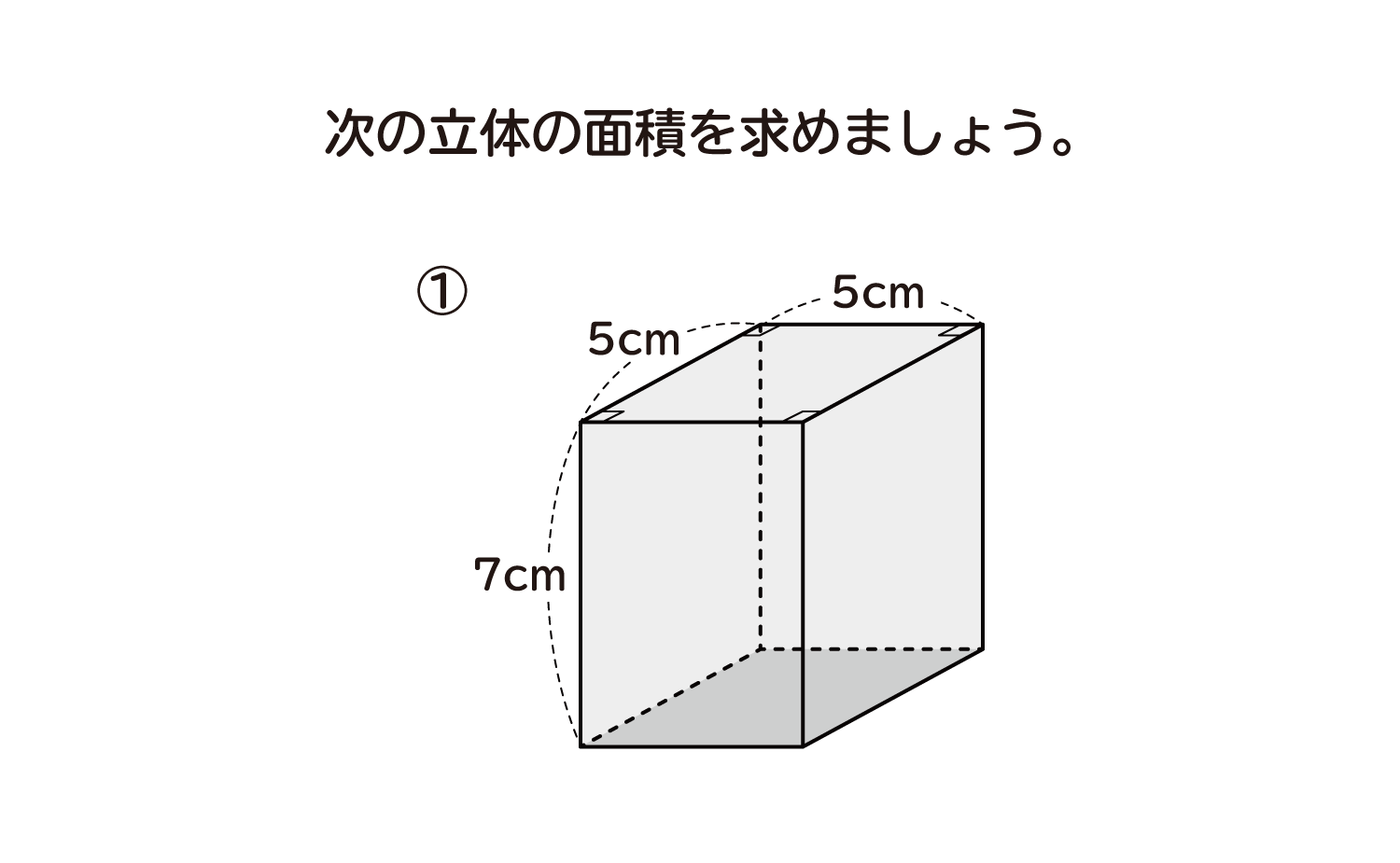
四角柱の体積と表面積の求め方 次は四角柱ですが、柱体はどれも同じ方針で進めてかまいません。 問題2- (2)次の四角柱の体積と表面積を求めなさい。 表面積を求めるために 展開図 を書きます。 そのとき、横にある面(側面)を長方形として横に広げて書きます。 上下の面(底面)はその長方形にひっつけてしまえば良いだけです。 ※ 柱体は上の面と下の面は合同になります。 どちらの面も『底 どちらも先ほどの公式が当てはまる、切頭四角柱であることがわかりますね。 赤い方の体積を 、青い方の体積を とすると、答えは以下の通りになります。 のように0が入っていても、問題なく公式が使えるというのがポイントです。 = + + + = + + + 前回の記事 ⇒ 三平方の定理が成り立つ三辺の比:最重要7パターン 次の記事 ⇒ 斜めに切断された三角柱の体積は、こう解くべし!
Incoming Term: 四角柱 体積の求め方,




0 件のコメント:
コメントを投稿